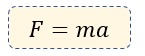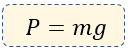La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo.
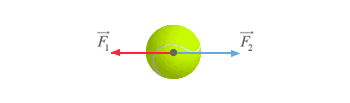
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m ·a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.
 Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m · v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:
La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
F = dp/dt
De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:
F = d(m·v)/dt = m·dv/dt + dm/dt ·v
Como la masa es constante
dm/dt = 0
y recordando la definición de aceleración, nos queda
F = m a
tal y como habíamos visto anteriormente.
Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:
0 = dp/dt
es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero. Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la derivada de una constante es cero). Esto es el Principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es nula, la cantidad de movimiento del cuerpo permanece constante en el tiempo.
Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en la cantidad de movimiento de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos.
Consecuentemente, hay relación entre la causa y el efecto, esto es, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.
La segunda ley de Newton para casos de masas constantes
Muchos de los casos que tienen interés práctico son los referidos a cuerpos que en su
movimiento mantienen su cantidad de materia, masa, aproximadamente constante; ya que en
ellos, la 2da ley de Newton tiene una forma particular de plantearse. En primer lugar, como ya
sabemos la cantidad de movimiento se puede calcular de la siguiente manera: P =m ⋅v , si la
sustituimos en la ecuación de la segunda ley nos queda:
∑ Fe= ∆ (mv) / ∆t
Como hemos considerado a la masa como un valor constante, podemos sacarla del
paréntesis que acompaña al símbolo de cambio (∆) quedando la ecuación de la siguiente manera.